Aplicaciones de Edge Impulse
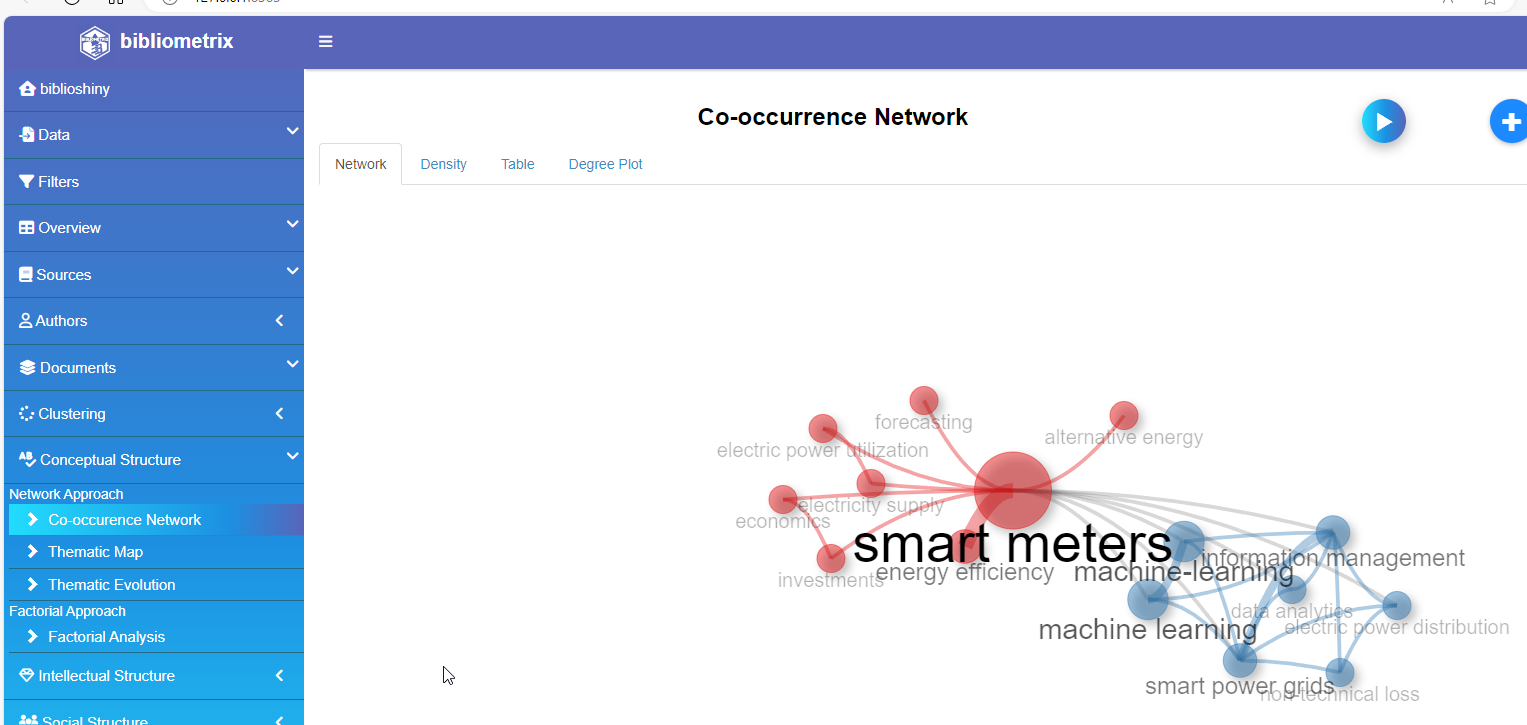
Edge Impulse es una plataforma que permite desarrollar e implementar fácilmente modelos de aprendizaje automático (IA) en dispositivos con recursos limitados, como microcontroladores y dispositivos del Internet de las cosas (IoT).