Evaluar modelos ingenuos para pronosticar el consumo de electricidad de los hogares

El conjunto de datos de ‘ Consumo de energía del hogar ‘ es un conjunto de datos de series de tiempo multivariable que describe el consumo de electricidad de un solo hogar durante cuatro años.

Los datos se recopilaron entre diciembre de 2006 y noviembre de 2010 y cada minuto se recopilaron observaciones del consumo de energía dentro del hogar.

Es una serie multivariada compuesta por siete variables (además de la fecha y la hora). Las variables son las siguientes:

• global_active_power : la potencia activa total consumida por el hogar (kilovatios).
• global_reactive_power : La potencia reactiva total consumida por el hogar (kilovatios).
• voltaje : Voltaje promedio (voltios).
• global_intensity : Intensidad de corriente promedio (amperios).
• sub_metering_1 : Energía activa para cocina (vatios-hora de energía activa).
• sub_metering_2 : Energía activa para lavandería (vatios-hora de energía activa).
• sub_metering_3 : Energía activa para sistemas de control climático (vatios-hora de energía activa).

La potencia aparente  o potencia total se subdividen en dos componentes, que son la potencia activa y la potencia reactiva, la primera de ellas es la que nos encontraremos en la factura de la luz de nuestra vivienda, (en la industria es diferente), cobrándonos unos bonitos €/kWh y por tanto será el que realmente importa si lo que queremos es ver cuanto nos cuesta hacer funcionar un aparato eléctrico. Por otro lado si la tensión y la corriente se desfasan porque la carga que tengo conectada así lo requiere (aparatos con bobinas en su interior), entonces aparece la famosa energía reactiva, que hace que la potencia aparente se diferencie bastante de la activa (la que nos cobran).

Para conocer el valor de la potencia reactiva (Q) es necesario conocer el desfase (phi) entre estas dos señales (voltaje y corriente) y aplicar la fórmula Q=V*I*sen(phi). Con la potencia activa sucede algo similar pero sustituyendo seno por coseno en la expresión.

Existen formas de compensar la energía reactiva (disminuirla), normalmente se basan en instalar condensadores que compensan las cargas inductivas (bobinas) con cargas capacitivas (condensadores), pero esto sólo se hace a nivel industrial ya que en el ámbito doméstico todavía (TODAVÍA) no pagamos por la reactiva consumida.

En nuestros cálculos se puede crear una cuarta variable de submedición restando la suma de tres variables de sub-medición definidas de la energía activa total de la siguiente manera:

sub_metering_remainder = (global_active_power * 1000 / 60) - (sub_metering_1 + sub_metering_2 + sub_metering_3)

Cargar y preparar conjunto de datos

El conjunto de datos se puede descargar desde el repositorio de UCI Machine Learning como un solo archivo .zip de unos 20 megabytes:consumo_electricidad_hogar.zip

Si descargamos el conjunto de datos y descomprimimos en su directorio de trabajo actual tendremos el archivo “ home_power_consumption.txt ” que tiene un tamaño de aproximadamente 127 megabytes y contiene todas las medidas.

Podemos usar la función read_csv() para cargar los datos y combinar las dos primeras columnas en una única columna de fecha y hora que podemos usar como índice.

# load all datadataset = read_csv('household_power_consumption.txt', sep=';', header=0, low_memory=False, infer_datetime_format=True, parse_dates={'datetime':[0,1]}, index_col=['datetime'])

A continuación, podemos marcar todos los valores faltantes indicados con un ‘ ? ‘ carácter con un valor NaN , que es un flotante.

Esto nos permitirá trabajar con los datos como una matriz de valores de punto flotante en lugar de tipos mixtos (menos eficientes).

# mark all missing valuesdataset.replace('?', nan, inplace=True)# make dataset numericdataset = dataset.astype('float32')

También necesitamos completar los valores faltantes ahora que han sido marcados.

Un enfoque muy simple sería copiar la observación a la misma hora del día anterior. Podemos implementar esto en una función llamada fill_missing() que tomará la matriz NumPy de los datos y copiará los valores de hace exactamente 24 horas.

# fill missing values with a value at the same time one day agodef fill_missing(values): one_day = 60 * 24 for row in range(values.shape[0]): for col in range(values.shape[1]): if isnan(values[row, col]): values[row, col] = values[row - one_day, col]

Podemos aplicar esta función directamente a los datos dentro del DataFrame.

# fill missingfill_missing(dataset.values)

Ahora podemos crear una nueva columna que contenga el resto de la submedición, utilizando el cálculo de la sección anterior.

# add a column for for the remainder of sub meteringvalues = dataset.valuesdataset['sub_metering_4'] = (values[:,0] * 1000 / 60) - (values[:,4] + values[:,5] + values[:,6])

Ahora podemos guardar la versión limpia del conjunto de datos en un nuevo archivo; en este caso, simplemente cambiaremos la extensión del archivo a .csv y guardaremos el conjunto de datos como ‘ home_power_consumption.csv ‘.

# save updated datasetdataset.to_csv('household_power_consumption.csv')

Uniendo todo esto, el ejemplo completo de cargar, limpiar y guardar el conjunto de datos se enumera a continuación.

# load and clean-up data
from numpy import nan
from numpy import isnan
from pandas import read_csv
from pandas import to_numeric
 
# fill missing values with a value at the same time one day ago
def fill_missing(values):
 one_day = 60 * 24
 for row in range(values.shape[0]):
 for col in range(values.shape[1]):
 if isnan(values[row, col]):
 values[row, col] = values[row - one_day, col]
 
# load all data
dataset = read_csv('household_power_consumption.txt', sep=';', header=0, low_memory=False, infer_datetime_format=True, parse_dates={'datetime':[0,1]}, index_col=['datetime'])
# mark all missing values
dataset.replace('?', nan, inplace=True)
# make dataset numeric
dataset = dataset.astype('float32')
# fill missing
fill_missing(dataset.values)
# add a column for for the remainder of sub metering
values = dataset.values
dataset['sub_metering_4'] = (values[:,0] * 1000 / 60) - (values[:,4] + values[:,5] + values[:,6])
# save updated dataset
dataset.to_csv('household_power_consumption.csv')

Al ejecutar el ejemplo, se crea el nuevo archivo » home_power_consumption.csv » que podemos usar como punto de partida para nuestro proyecto de modelado.

Evaluación del modelo

Ahora consideraremos cómo podemos desarrollar y evaluar modelos predictivos para el conjunto de datos de energía doméstica que ya hemos preparadio. Para ello estudiaremos cuatro aspectos:

1. Encuadre del problema.
2. Métrica de evaluación.
3. Conjuntos de entrenamiento y prueba.
4. Validación Walk-Forward.

Encuadre del problema

Hay muchas maneras de aprovechar y explorar el conjunto de datos de consumo de energía del hogar. En este estudio, usaremos los datos para explorar una pregunta muy específica; esto es: Dado el consumo de energía reciente, ¿Cuál es el consumo de energía esperado para la próxima semana?

Esto requiere que un modelo predictivo pronostique la potencia activa total para cada día durante los próximos siete días. Técnicamente, este encuadre del problema se conoce como un problema de pronóstico de serie de tiempo de múltiples pasos, dados los múltiples pasos de pronóstico. Un modelo que hace uso de múltiples variables de entrada puede denominarse modelo de pronóstico de serie de tiempo multivariante de múltiples pasos.

Un modelo de este tipo podría ser útil dentro del hogar en la planificación de gastos. También podría ser útil desde el punto de vista de la oferta para planificar la demanda de electricidad de un hogar específico.

Este marco del conjunto de datos también sugiere que sería útil reducir la muestra de las observaciones por minuto del consumo de energía a los totales diarios. Esto no es obligatorio, pero tiene sentido, dado que estamos interesados ​​en la potencia total por día.

Podemos lograr esto fácilmente usando la función resample() en pandas DataFrame. Llamar a esta función con el argumento ‘ D ‘ permite que los datos cargados indexados por fecha y hora se agrupen por día . Luego podemos calcular la suma de todas las observaciones para cada día y crear un nuevo conjunto de datos de consumo de energía diario para cada una de las ocho variables.

El ejemplo completo se muestra a continuación.

# resample minute data to total for each day
from pandas import read_csv
# load the new file
dataset = read_csv('household_power_consumption.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])
# resample data to daily
daily_groups = dataset.resample('D')
daily_data = daily_groups.sum()
# summarize
print(daily_data.shape)
print(daily_data.head())
# save
daily_data.to_csv('household_power_consumption_days.csv')

Al ejecutar el ejemplo, se crea un nuevo conjunto de datos de consumo de energía total diario y se guarda el resultado en un archivo separado llamado » home_power_conquisition_days.csv «.

Podemos usar esto como el conjunto de datos para ajustar y evaluar modelos predictivos para el marco elegido del problema.

Métrica de evaluación

Un pronóstico estará compuesto por siete valores, uno para cada día de la semana siguiente. Es común con los problemas de pronóstico de varios pasos evaluar cada paso de tiempo pronosticado por separado. Esto es útil por varias razones:

• Para comentar sobre la aptitud en un plazo de entrega específico (p. ej., +1 día frente a +3 días).
• Para contrastar modelos en función de sus habilidades en diferentes plazos de entrega (por ejemplo, modelos buenos en +1 día frente a modelos buenos en días +5).

Las unidades de la potencia total son los kilovatios y sería útil tener una métrica de error que también estuviera en las mismas unidades. Tanto el error cuadrático medio (RMSE) como el error absoluto medio (MAE) se ajustan a esta factura, aunque RMSE se usa más comúnmente y se adoptará en esta visión. A diferencia de MAE, RMSE castiga más los errores de pronóstico.

La métrica de rendimiento para este problema será el RMSE para cada tiempo de entrega desde el día 1 hasta el día 7.

Como atajo, puede ser útil resumir el rendimiento de un modelo utilizando una puntuación única para ayudar en la selección del modelo.

Una puntuación posible que podría usarse sería el RMSE en todos los días de pronóstico.

La función Evaluation_forecasts() a continuación implementará este comportamiento y devolverá el rendimiento de un modelo basado en múltiples pronósticos de siete días.

# evaluate one or more weekly forecasts against expected values
def evaluate_forecasts(actual, predicted):
 scores = list()
 # calculate an RMSE score for each day
 for i in range(actual.shape[1]):
 # calculate mse
 mse = mean_squared_error(actual[:, i], predicted[:, i])
 # calculate rmse
 rmse = sqrt(mse)
 # store
 scores.append(rmse)
 # calculate overall RMSE
 s = 0
 for row in range(actual.shape[0]):
 for col in range(actual.shape[1]):
 s += (actual[row, col] - predicted[row, col])**2
 score = sqrt(s / (actual.shape[0] * actual.shape[1]))
 return score, scores

Ejecutar la función primero devolverá el RMSE general independientemente del día, luego una matriz de puntajes de RMSE para cada día.

Conjuntos de entrenamiento y prueba

Usaremos los primeros tres años de datos para entrenar modelos predictivos y el último año para evaluar modelos.

Los datos de un conjunto de datos determinado se dividirán en semanas estándar (son semanas que comienzan en domingo y terminan en sábado).

Esta es una forma realista y útil de usar el encuadre elegido del modelo, donde se puede predecir el consumo de energía para la próxima semana. También es útil con el modelado, donde los modelos se pueden usar para predecir un día específico (por ejemplo, el miércoles) o la secuencia completa.

Dividiremos los datos en semanas estándar, trabajando hacia atrás desde el conjunto de datos de prueba.

El último año de los datos es 2010 y el primer domingo de 2010 fue el 3 de enero. Los datos terminan a mediados de noviembre de 2010 y el último sábado más cercano en los datos es el 20 de noviembre. Esto da 46 semanas de datos de prueba.

La primera y la última fila de datos diarios para el conjunto de datos de prueba se proporcionan a continuación para su confirmación.

2010-01-03,2083.4539999999984,191.61000000000055,350992.12000000034,8703.600000000033,3842.0,4920.0,10074.0,15888.233355799992
...
2010-11-20,2197.006000000004,153.76800000000028,346475.9999999998,9320.20000000002,4367.0,2947.0,11433.0,17869.76663959999

Los datos diarios comienzan a finales de 2006.

El primer domingo en el conjunto de datos es el 17 de diciembre, que es la segunda fila de datos.

La organización de los datos en semanas estándar proporciona 159 semanas estándar completas para entrenar un modelo predictivo.

2006-12-17,3390.46,226.0059999999994,345725.32000000024,14398.59999999998,2033.0,4187.0,13341.0,36946.66673200004
...
2010-01-02,1309.2679999999998,199.54600000000016,352332.8399999997,5489.7999999999865,801.0,298.0,6425.0,14297.133406600002

La función split_dataset() a continuación divide los datos diarios en conjuntos de entrenamiento y prueba y organiza cada uno en semanas estándar.

Se utilizan compensaciones de fila específicas para dividir los datos utilizando el conocimiento del conjunto de datos. Luego, los conjuntos de datos divididos se organizan en datos semanales mediante la función NumPy split() .

# split a univariate dataset into train/test sets
def split_dataset(data):
 # split into standard weeks
 train, test = data[1:-328], data[-328:-6]
 # restructure into windows of weekly data
 train = array(split(train, len(train)/7))
 test = array(split(test, len(test)/7))
 return train, test

Podemos probar esta función cargando el conjunto de datos diario e imprimiendo la primera y la última fila de datos tanto del tren como de los conjuntos de prueba para confirmar que cumplen con las expectativas anteriores.

El ejemplo de código completo se muestra a continuación.

# split into standard weeks
from numpy import split
from numpy import array
from pandas import read_csv
 
# split a univariate dataset into train/test sets
def split_dataset(data):
 # split into standard weeks
 train, test = data[1:-328], data[-328:-6]
 # restructure into windows of weekly data
 train = array(split(train, len(train)/7))
 test = array(split(test, len(test)/7))
 return train, test
 
# load the new file
dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])
train, test = split_dataset(dataset.values)
# validate train data
print(train.shape)
print(train[0, 0, 0], train[-1, -1, 0])
# validate test
print(test.shape)
print(test[0, 0, 0], test[-1, -1, 0])

Ejecutar el ejemplo muestra que, de hecho, el conjunto de datos del tren tiene 159 semanas de datos, mientras que el conjunto de datos de prueba tiene 46 semanas.

Podemos ver que la potencia activa total para el tren y el conjunto de datos de prueba para la primera y la última fila coinciden con los datos de las fechas específicas que definimos como los límites de las semanas estándar para cada conjunto.

(159, 7, 8)
3390.46 1309.2679999999998
(46, 7, 8)
2083.4539999999984 2197.006000000004

Validación Walk-Forward

Los modelos se evaluarán utilizando un esquema llamado validación de avance . Aquí es donde se requiere que un modelo haga una predicción de una semana, luego los datos reales de esa semana se ponen a disposición del modelo para que pueda usarse como base para hacer una predicción en la semana siguiente. Esto es tanto realista en cuanto a cómo se puede usar el modelo en la práctica como beneficioso para los modelos, permitiéndoles hacer uso de los mejores datos disponibles.

Podemos demostrar esto a continuación con la separación de los datos de entrada y los datos de salida/predichos.

Input, Predict
[Week1] Week2
[Week1 + Week2] Week3
[Week1 + Week2 + Week3] Week4
...

El enfoque de validación de avance para evaluar modelos predictivos en este conjunto de datos se implementa a continuación y se llama evaluar_modelo() .

El nombre de una función se proporciona para el modelo como el argumento » model_func «. Esta función es responsable de definir el modelo, ajustar el modelo a los datos de entrenamiento y hacer un pronóstico de una semana.

Los pronósticos hechos por el modelo luego se evalúan contra el conjunto de datos de prueba utilizando la función de evaluación_previsiones() previamente definida .

# evaluate a single model
def evaluate_model(model_func, train, test):
 # history is a list of weekly data
 history = [x for x in train]
 # walk-forward validation over each week
 predictions = list()
 for i in range(len(test)):
 # predict the week
 yhat_sequence = model_func(history)
 # store the predictions
 predictions.append(yhat_sequence)
 # get real observation and add to history for predicting the next week
 history.append(test[i, :])
 predictions = array(predictions)
 # evaluate predictions days for each week
 score, scores = evaluate_forecasts(test[:, :, 0], predictions)
 return score, scores

Una vez que tenemos la evaluación de un modelo, podemos resumir el rendimiento.

La función a continuación denominada resume_scores() mostrará el rendimiento de un modelo en una sola línea para facilitar la comparación con otros modelos.

# summarize scores
def summarize_scores(name, score, scores):
 s_scores = ', '.join(['%.1f' % s for s in scores])
 print('%s: [%.3f] %s' % (name, score, s_scores))

Ahora tenemos todos los elementos para comenzar a evaluar modelos predictivos en el conjunto de datos.

Modelos de pronóstico ingenuos

Es importante probar modelos de pronóstico ingenuos en cualquier problema de predicción nuevo. Los resultados de los modelos ingenuos brindan una idea cuantitativa de cuán difícil es el problema de pronóstico y brindan un rendimiento de línea de base mediante el cual se pueden evaluar métodos de pronóstico más sofisticados.

Ahora desarrollaremos y compararemos tres métodos de pronóstico ingenuos para el problema de predicción de energía doméstica; ellos son:

• Pronóstico de Persistencia Diaria.
• Pronóstico persistente semanal.
• Pronóstico persistente semanal de hace un año.

Previsión de persistencia diaria

El primer pronóstico ingenuo que desarrollaremos es un modelo de persistencia diaria. Este modelo toma la potencia activa del último día anterior al período de pronóstico (por ejemplo, el sábado) y la utiliza como el valor de la potencia para cada día del período de pronóstico (de domingo a sábado).

La función daily_persistence() a continuación implementa la estrategia de pronóstico de persistencia diaria.

# daily persistence model
def daily_persistence(history):
 # get the data for the prior week
 last_week = history[-1]
 # get the total active power for the last day
 value = last_week[-1, 0]
 # prepare 7 day forecast
 forecast = [value for _ in range(7)]
 return forecast

Pronóstico persistente semanal

Otro buen pronóstico ingenuo al pronosticar una semana estándar es usar toda la semana anterior como pronóstico para la próxima semana. Se basa en la idea de que la próxima semana será muy similar a esta semana.

La funciónweekly_persistence() a continuación implementa la estrategia de pronóstico de persistencia semanal.

# weekly persistence model
def weekly_persistence(history):
 # get the data for the prior week
 last_week = history[-1]
 return last_week[:, 0]

Pronóstico persistente semanal de hace un año

Similar a la idea de usar la semana pasada para pronosticar la próxima semana es la idea de usar la misma semana del año pasado para predecir la próxima semana. Es decir, utilizar la semana de observaciones de hace 52 semanas como pronóstico, basándose en la idea de que la próxima semana será similar a la misma semana de hace un año.

La siguiente función week_one_year_ago_persistence() implementa la estrategia de pronóstico de la semana de hace un año.

# week one year ago persistence model
def week_one_year_ago_persistence(history):
 # get the data for the prior week
 last_week = history[-52]
 return last_week[:, 0]

Comparación de modelos ingenuos

Podemos comparar cada una de las estrategias de pronóstico utilizando el arnés de prueba desarrollado en la sección anterior.

En primer lugar, el conjunto de datos se puede cargar y dividir en conjuntos de entrenamiento y de prueba.

# load the new filedataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])# split into train and testtrain, test = split_dataset(dataset.values)

Cada una de las estrategias se puede almacenar en un diccionario con un nombre único. Este nombre se puede utilizar en la impresión y en la creación de un gráfico de las partituras.

# define the names and functions for the models we wish to evaluatemodels = dict()models['daily'] = daily_persistencemodels['weekly'] = weekly_persistencemodels['week-oya'] = week_one_year_ago_persistence

Luego, podemos enumerar cada una de las estrategias, evaluarlas mediante la validación de avance, imprimir los puntajes y agregar los puntajes a un gráfico de líneas para una comparación visual.

# evaluate each modeldays = ['sun', 'mon', 'tue', 'wed', 'thr', 'fri', 'sat']for name, func in models.items(): # evaluate and get scores score, scores = evaluate_model(func, train, test) # summarize scores summarize_scores('daily persistence', score, scores) # plot scores pyplot.plot(days, scores, marker='o', label=name)

Uniendo todo esto, el ejemplo completo que evalúa las tres estrategias de pronóstico ingenuo se enumera a continuación.

# naive forecast strategies
from math import sqrt
from numpy import split
from numpy import array
from pandas import read_csv
from sklearn.metrics import mean_squared_error
from matplotlib import pyplot
 
# split a univariate dataset into train/test sets
def split_dataset(data):
 # split into standard weeks
 train, test = data[1:-328], data[-328:-6]
 # restructure into windows of weekly data
 train = array(split(train, len(train)/7))
 test = array(split(test, len(test)/7))
 return train, test
 
# evaluate one or more weekly forecasts against expected values
def evaluate_forecasts(actual, predicted):
 scores = list()
 # calculate an RMSE score for each day
 for i in range(actual.shape[1]):
 # calculate mse
 mse = mean_squared_error(actual[:, i], predicted[:, i])
 # calculate rmse
 rmse = sqrt(mse)
 # store
 scores.append(rmse)
 # calculate overall RMSE
 s = 0
 for row in range(actual.shape[0]):
 for col in range(actual.shape[1]):
 s += (actual[row, col] - predicted[row, col])**2
 score = sqrt(s / (actual.shape[0] * actual.shape[1]))
 return score, scores
 
# summarize scores
def summarize_scores(name, score, scores):
 s_scores = ', '.join(['%.1f' % s for s in scores])
 print('%s: [%.3f] %s' % (name, score, s_scores))
 
# evaluate a single model
def evaluate_model(model_func, train, test):
 # history is a list of weekly data
 history = [x for x in train]
 # walk-forward validation over each week
 predictions = list()
 for i in range(len(test)):
 # predict the week
 yhat_sequence = model_func(history)
 # store the predictions
 predictions.append(yhat_sequence)
 # get real observation and add to history for predicting the next week
 history.append(test[i, :])
 predictions = array(predictions)
 # evaluate predictions days for each week
 score, scores = evaluate_forecasts(test[:, :, 0], predictions)
 return score, scores
 
# daily persistence model
def daily_persistence(history):
 # get the data for the prior week
 last_week = history[-1]
 # get the total active power for the last day
 value = last_week[-1, 0]
 # prepare 7 day forecast
 forecast = [value for _ in range(7)]
 return forecast
 
# weekly persistence model
def weekly_persistence(history):
 # get the data for the prior week
 last_week = history[-1]
 return last_week[:, 0]
 
# week one year ago persistence model
def week_one_year_ago_persistence(history):
 # get the data for the prior week
 last_week = history[-52]
 return last_week[:, 0]
 
# load the new file
dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])
# split into train and test
train, test = split_dataset(dataset.values)
# define the names and functions for the models we wish to evaluate
models = dict()
models['daily'] = daily_persistence
models['weekly'] = weekly_persistence
models['week-oya'] = week_one_year_ago_persistence
# evaluate each model
days = ['sun', 'mon', 'tue', 'wed', 'thr', 'fri', 'sat']
for name, func in models.items():
 # evaluate and get scores
 score, scores = evaluate_model(func, train, test)
 # summarize scores
 summarize_scores(name, score, scores)
 # plot scores
 pyplot.plot(days, scores, marker='o', label=name)
# show plot
pyplot.legend()
pyplot.show()

Al ejecutar el ejemplo, primero se imprimen las puntuaciones totales y diarias de cada modelo. Podemos ver que la estrategia semanal funciona mejor que la estrategia diaria y que la semana de hace un año ( week-oya ) vuelve a funcionar ligeramente mejor.

Nota : Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.

Podemos ver esto tanto en los puntajes generales de RMSE para cada modelo como en los puntajes diarios para cada día de pronóstico. Una excepción es el error de pronóstico del primer día (domingo), donde parece que el modelo de persistencia diaria funciona mejor que las estrategias de dos semanas.

Podemos usar la estrategia semana-oya con un RMSE general de 465,294 kilovatios como referencia de rendimiento para que los modelos más sofisticados se consideren hábiles en este marco específico del problema.

daily: [511.886] 452.9, 596.4, 532.1, 490.5, 534.3, 481.5, 482.0
weekly: [469.389] 567.6, 500.3, 411.2, 466.1, 471.9, 358.3, 482.0
week-oya: [465.294] 550.0, 446.7, 398.6, 487.0, 459.3, 313.5, 555.1

También se crea un diagrama de líneas del error de pronóstico diario.

Podemos ver el mismo patrón observado de las estrategias semanales que funcionan mejor que la estrategia diaria en general, excepto en el caso del primer día.

Es sorprendente que la semana de hace un año funcione mejor que la semana anterior porque parece mas lógico esperar que el consumo de energía de la semana pasada fuera más relevante.

La revisión de todas las estrategias en el mismo gráfico sugiere posibles combinaciones de estrategias que pueden dar como resultado un rendimiento aún mejor.

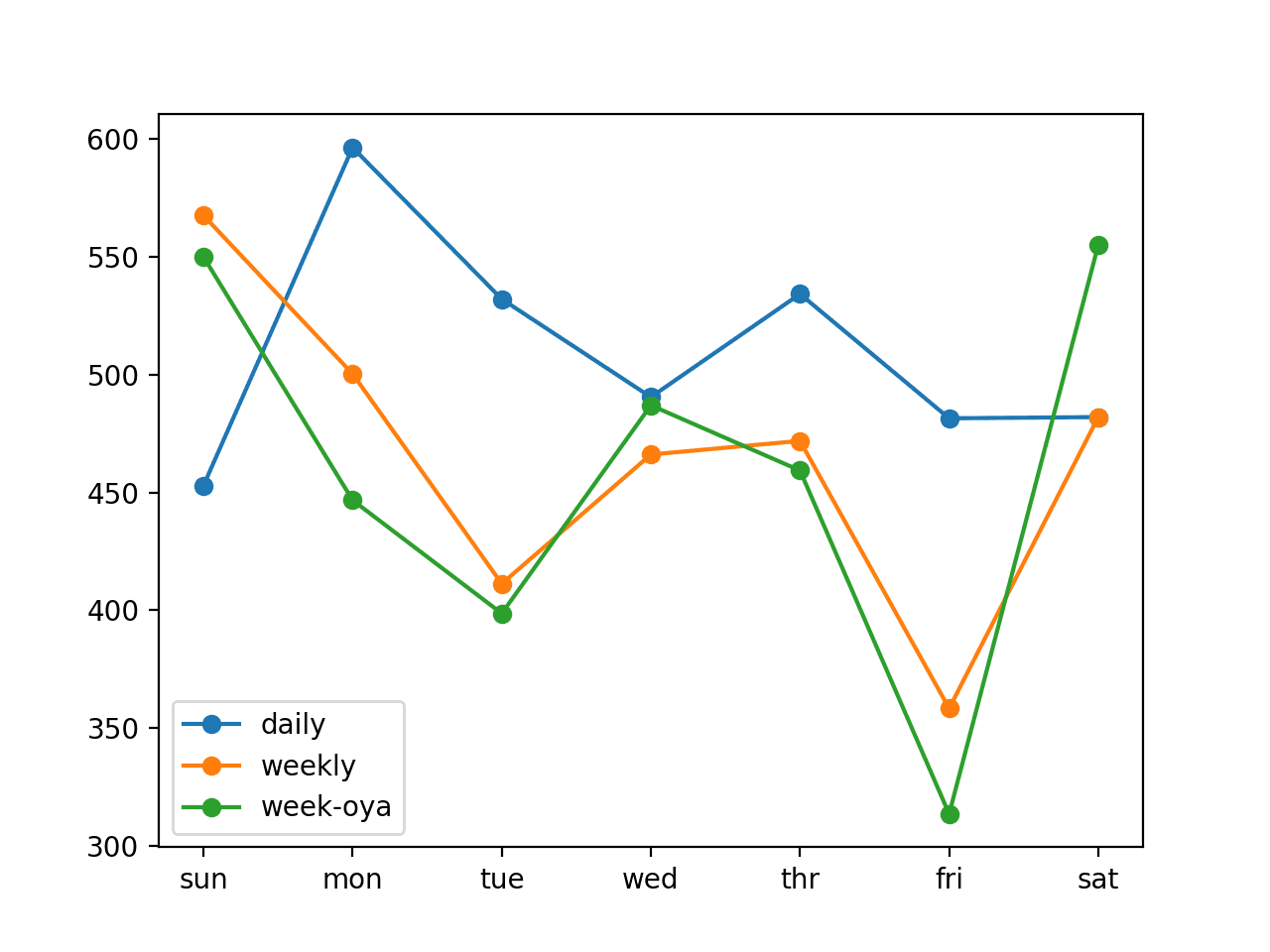
Gráfica de líneas que compara estrategias de pronóstico ingenuo para el pronóstico de energía doméstica

Extensiones

Hay algunas ideas para ampliar el contenido que hemos visto que tal vez desee explorar.

• Estrategia ingenua adicional . Proponer, desarrollar y evaluar una estrategia ingenua más para pronosticar el consumo de energía de la próxima semana.
• Estrategia de conjunto ingenua . Desarrollar una estrategia de conjunto que combine las predicciones de los tres métodos de pronóstico ingenuo propuestos.
• Modelos optimizados de persistencia directa . Probar y encontrar el día anterior relativo óptimo (por ejemplo, -1 o -7) para usar para cada día de pronóstico en un modelo de persistencia directa.

Fuente: https://machinelearningmastery.com/naive-methods-for-forecasting-household-electricity-consumption/