¿Alguna vez te has preguntado cómo funciona el asistente de voz en tu teléfono? Pues bien , los HMM modelan los datos como una secuencia. Tomemos un ejemplo para entender por qué tiene sentido modelar como secuencia. Una frase como «Me gusta jugar a…» suele ser seguida por palabras como «guitarra», «fútbol», etc. En estos ejemplos, la palabra anterior nos ayuda a predecir mejor la siguiente palabra o palabras. Esto es un ejemplo de modelado de lenguaje, pero hay muchísimo mas ejemplos como puede ser en la desagregación del consumo energético (por ejemplo se supone una lampara esta encendida y seguirá así en los siguientes estadas cambiando solo en la transición de encendida a apagado o viceversa), donde destaca el algoritmo FHMM (Factorial oculto de Markoff) por su precisión y relativo poco coste computacional.
Las Cadenas de Markov describen matemáticamente una secuencia de eventos posibles. La probabilidad de cada evento depende de eventos pasados. En este artículo, hablamos de las cadenas de Markov, los Modelos Ocultos de Markov y los problemas clave de los HMM.

Cadenas de Markov
Una cadena de Markov es uno de los modelos de Markov más simples. Esta cadena asume que una observación depende solo de la observación inmediatamente anterior. En otras palabras, dado el estado presente, el futuro es independiente del pasado.
El modelo gráfico de una cadena de Markov muestra nodos (estados) y flechas que indican dependencias entre estados consecutivos.
La probabilidad conjunta de una secuencia se calcula como:
P(x1,x2,…,xt+1)=P(x1)P(x2∣x1)P(x3∣x2)…P(xt+1∣xt)
Ejemplos de Cadenas de Markov
- Clima Soleado y Lluvioso: El clima del día siguiente depende del clima del día anterior. Por ejemplo, un día soleado puede ser seguido por un día lluvioso con cierta probabilidad.
- Cambio de Monedas Justa y Sesgada: Se tiene una moneda justa y una sesgada; la moneda elegida en un instante depende de la moneda elegida en el instante anterior.
- Estado de un Aire Acondicionado: El compresor puede estar encendido o apagado, y el estado en un momento depende del estado anterior.
Parámetros de una Cadena de Markov
- Matriz de transición AAA: Probabilidades de pasar de un estado a otro.
- Distribución inicial π\piπ: Probabilidades de los estados iniciales.
Modelos Ocultos de Markov (HMM)
En un HMM, el estado real (oculto) no es observable directamente, pero genera observaciones visibles. Por ejemplo:
- Clima oculto y observación: No ves el clima, pero observas si los zapatos de tu compañero están mojados o secos.
- Moneda oculta y observación: No sabes qué moneda se lanzó, solo ves el resultado (cara o cruz).
- Estado del compresor y observación: No sabes si el compresor está encendido, pero observas el consumo de energía.
Componentes de un HMM
- Estados ocultos ztz_tzt: Variables no observables que evolucionan según una cadena de Markov.
- Observaciones xtx_txt: Datos visibles generados por los estados ocultos.
- Parámetros:
- Matriz de transición AAA
- Distribución inicial π\piπ
- Probabilidad de emisión ϕ\phiϕ (probabilidad de observar xtx_txt dado el estado oculto ztz_tzt)
Ejemplo de Probabilidades de Emisión
- En un día soleado, los zapatos pueden estar mojados con probabilidad 0.2 (por ejemplo, por un aspersor).
- En un día lluvioso, los zapatos están mojados con probabilidad 0.9.
Algoritmos Clave en HMM
- Algoritmo Forward: Calcula eficientemente la probabilidad de observar una secuencia dada la configuración del HMM, usando programación dinámica para evitar cálculos repetidos.
- Algoritmo Backward: Similar al Forward, calcula la probabilidad de observar la secuencia futura desde un estado dado.
Problemas Fundamentales en HMM
- Evaluación: Calcular la probabilidad de una secuencia de observaciones dada la configuración del HMM.
- Decodificación: Encontrar la secuencia más probable de estados ocultos que generó las observaciones.
- Aprendizaje: Ajustar los parámetros del HMM para maximizar la probabilidad de las observaciones.
Diferencias entre cadenas de Markov y HMM
Las principales diferencias entre cadenas de Markov y modelos ocultos de Markov (HMM) son las siguientes:
| Aspecto | Cadena de Markov | Modelo Oculto de Markov (HMM) |
|---|---|---|
| Visibilidad de estados | Los estados son directamente observables. | Los estados son ocultos, no se observan directamente; solo se observan variables influenciadas por esos estados. |
| Datos observados | Se observa la secuencia de estados reales. | Se observa una secuencia de símbolos o datos generados probabilísticamente por los estados ocultos. |
| Parámetros del modelo | Solo se modelan las probabilidades de transición entre estados. | Se modelan probabilidades de transición entre estados ocultos y probabilidades de emisión (observación) condicionadas a esos estados. |
| Objetivo principal | Describir la evolución de estados observables. | Inferir la secuencia más probable de estados ocultos a partir de las observaciones visibles. |
| Complejidad y uso | Más simple, adecuado cuando los estados son conocidos. | Más complejo, útil cuando los estados no son accesibles directamente, como en reconocimiento de voz, bioinformática o procesamiento de lenguaje natural. |
En resumen, la cadena de Markov asume que el estado actual es visible y la transición depende solo del estado anterior, mientras que el modelo oculto de Markov añade una capa de incertidumbre: los estados reales son invisibles y solo se observan resultados relacionados probabilísticamente con esos estados ocultos, lo que requiere métodos para inferir dichos estados a partir de las observaciones.
Algoritmos clave en Modelos Ocultos de Markov (HMM)
Cálculo eficiente de la probabilidad de observación: Algoritmo Forward
Para calcular la probabilidad de observar una secuencia dada X={x1,x2,…,xT}bajo un HMM con parámetros θ={π,A,ϕ}, considerar todas las posibles secuencias ocultas tiene complejidad exponencial, ya que hay KTKT posibles caminos (donde KK es el número de estados ocultos y TT la longitud de la secuencia).
Para resolver esto, se usa el Algoritmo Forward, que es un método de programación dinámica que evita cálculos repetidos. Define:αt(i)=P(x1:t,zt=i∣θ)
Es decir, la probabilidad de observar la secuencia hasta el tiempo tt y estar en el estado oculto ii en el tiempo tt.
La relación recursiva es:
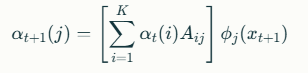
Donde:
- Aij es la probabilidad de transición del estado ii al estado j.
- ϕj(xt+1) es la probabilidad de emitir la observación xt+1 desde el estado j.
La probabilidad total de la secuencia se obtiene sumando sobre todos los estados finales:P(X∣θ)=∑i=1KαT(i)
Algoritmo Backward
Complementa al algoritmo Forward calculando la probabilidad de observar la secuencia futura desde un estado oculto dado en un tiempo especifico. Calcula la probabilidad de observar la secuencia futura desde un estado dado en un tiempo específico.
βt(i)=P(xt+1,xt+2,…,xT∣zt=i,θ)
Es la probabilidad de observar la secuencia desde el tiempo t+1 hasta T, dado que en el tiempo t estamos en el estado i.
La relación recursiva es
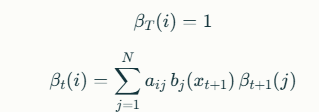
Con la condición base βT(i)=1 para todos los estados i.El algoritmo Backward junto con Forward permite calcular probabilidades posteriores y es base para otros algoritmos
Aplicaciones de Forward y Backward
Estos algoritmos se usan para:
- Calcular la probabilidad total de una secuencia observada.
- Estimar la probabilidad de estar en un estado oculto específico en un tiempo dado.
- Formar la base para otros algoritmos, como el algoritmo de Viterbi (para decodificación) y el algoritmo de Baum-Welch (para aprendizaje de parámetros).
Estos algoritmos permiten manejar la complejidad computacional y trabajar con secuencias largas y modelos con múltiples estados ocultos de manera eficiente.
Algoritmo de Viterbi
Este algoritmo encuentra la secuencia más probable de estados ocultos Z=(z1,z2,…,zT)Z=(z1,z2,…,zT) que generó la secuencia observada XX.
Define:
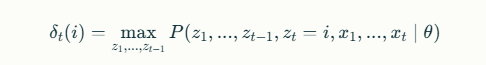
que es la probabilidad máxima de una secuencia de estados terminando en ii en el tiempo t.
Se calcula recursivamente:
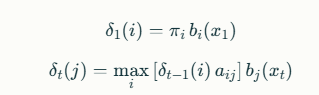
Durante la recursión se guarda la trayectoria que maximiza la probabilidad para reconstruir la secuencia óptima al final. Al concluir, se selecciona el estado con mayor δT(i) y se retrocede para obtener la secuencia completa de estados ocultos más probable
Algoritmo de Aprendizaje de Parámetros (Expectation-Maximization / Baum-Welch)
Cuando los estados ocultos no son conocidos, se usa el algoritmo EM para estimar los parámetros θ=(π,A,B)que maximizan la probabilidad de las observaciones.
- E-step (Esperanza): Utilizando los algoritmos Forward y Backward, se calcula la probabilidad posterior de estar en un estado dado en cada tiempo y la probabilidad de transitar entre estados en tiempos consecutivos.
- M-step (Maximización): Se actualizan los parámetros con base en estas probabilidades esperadas:
- La distribución inicial πi se actualiza con la probabilidad de estar en el estado ii en el tiempo 1.
- La matriz de transición aij se actualiza con la frecuencia esperada de transiciones del estado i al j.
- Las probabilidades de emisión bj(k) se actualizan con la frecuencia esperada de observar el símbolo k en el estado j.
Este proceso iterativo continúa hasta convergencia, ajustando el modelo para explicar mejor las observaciones.
Estos algoritmos son fundamentales para la aplicación práctica de los HMM en áreas como reconocimiento de voz, procesamiento del lenguaje natural, bioinformática y análisis de series temporales, permitiendo manejar la incertidumbre de estados ocultos y aprender modelos a partir de datos observables.
Resumen
En este post hemos visto una pequeña introducción sobre los Modelos Ocultos de Markov (HMM), comenzando con una explicación de las Cadenas de Markov y sus parámetros, como la matriz de transición y la probabilidad previa. Luego, ya mas en detalle hemos visto la diferencia clave de los estados «ocultos» que generan «observaciones» y sus tres parámetros fundamentales: la matriz de transición, la probabilidad previa y la probabilidad de emisión. Finalmente, hemos visto sucientamentea los algoritmos clave para trabajar con HMM, incluyendo el algoritmo de Avance, el algoritmo de Retroceso, el algoritmo de Viterbi para inferir la secuencia de estados ocultos más probable, y el algoritmo de aprendizaje de parámetros (Expectation-Maximization) cuando los estados ocultos son desconocidos.
Finalmente hemos visto las aplicaciones históricas de los HMM y su relación con los modelos de redes neuronales recurrentes (RNN) modernos. Por cierto, esta página ofrece además diagramas, ejemplos interactivos y explicaciones detalladas para entender cómo funcionan los modelos ocultos de Markov y sus aplicaciones en problemas reales como reconocimiento de voz, análisis de series temporales, y más.
Debe estar conectado para enviar un comentario.